CSLU2850.Lo1 Web Project 8

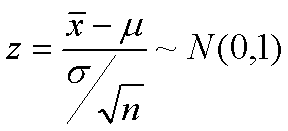
Assigned: April 2
Due: April 9

• work with z-Test Statistics;
• work with z-Values;

z-Test Statistics and z-Values

Standard Normal Curve

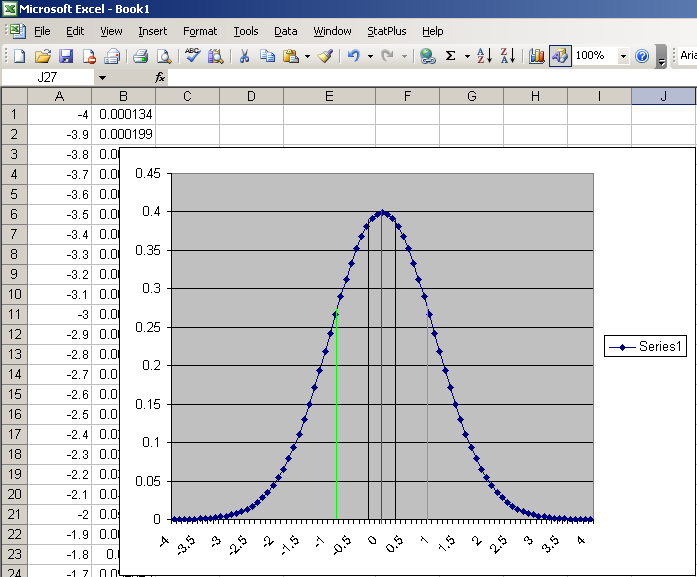
First, we must review the Standard Normal Curve, as it will be useful with this project. A Standard Normal Curve is a normal distribution with μ = 0 and σ = 1.

z-Test Statistics

A z-Test Statistic allows us to express a sampling distribution of the sample average in terms of a standard normal distribution. To do this, we must subtract μ from the sample average, then divide by the standard error. We can write this as:

One sided z-Value

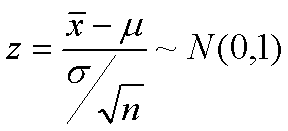
A z-Value, usually written z_p, is a value on the standard normal curve such that p-percent of the area under the curve is to the left of this value. Another way to write this is the point z on a standard normal curve such that:

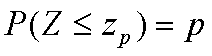
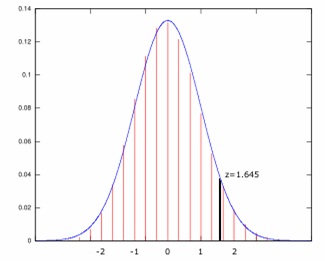
For example, z_0.95 = 1.645, so 95% of the area under the curve is to the left of 1.645:

Two sided z-Values

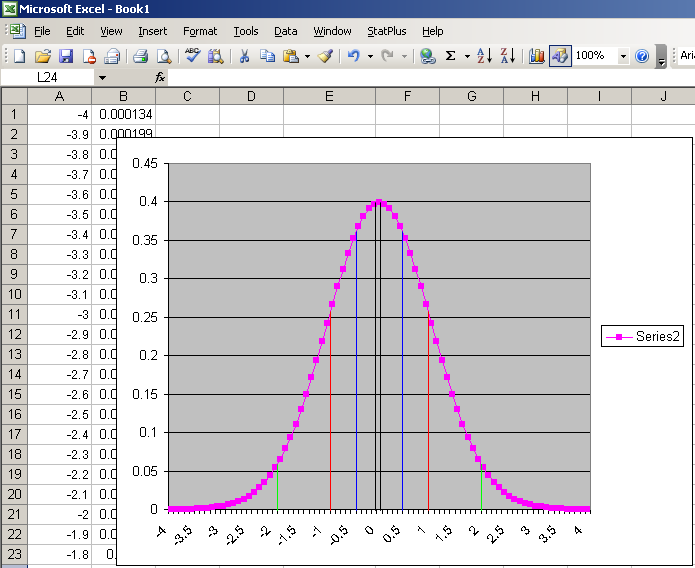
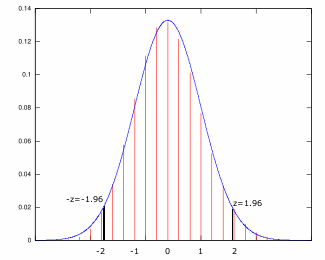
Two sided z-Values are similar to One sided z-Values, except the probability p, is the probability of the value falling in the center of the distribution. We also introduce another value, α, which is the probability that the value falls in one of the tails:

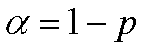
For the two-sided range of size p, the z-Values are -z_1-α/2 and z_1-α/2. In other words, for a random variable Z:

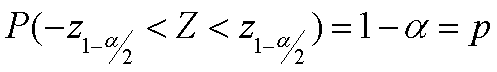
For example, if we want to find the central 95% of the standard normal curve, p=0.95, α=0.05, and z_0.975 = 1.96. So, 95% of the values on a standard normal curve lie between -1.96 and 1.96:

Now, we can use our Two-sided z-Values to construct a general expression for the confidence interval:

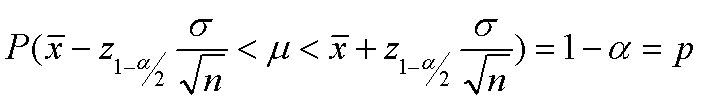
So, the upper and lower confidence limits for μ are:

Excel Functions

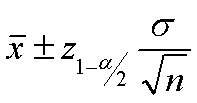
To calculate the value of z_p in Excel, use the function:

		=NORMSINV(k)
			where k = p;
			

To find the probability associated with a z-test statistic, use the function:

		=NORMSDIST(k)
			where k is the z-Test Statistic;
			

To find the y-value for a normal distribution:

		
		=NORMDIST(k,μ,σ,FALSE)
			where k is the x-value;
			

Deliverable

One Sided z-Values

1. First, plot a Standard Normal Curve, in the range [-4,4] in 0.1 intervals.
2. Draw a line to represent μ
3. Next calculate the one sided z-Values:
   1. z_0.2
   2. z_0.4
   3. z_0.6
   4. z_0.8
4. Plot the z-Values that you calculated in the last part on the Standard Normal Curve. Use two colors, one for z_0.2 and z_0.8, the other for z_0.4 and z_0.6.

Two Sided z-Values

1. Plot another Standard Normal Curve, in the range [-4,4] in 0.1 intervals.
2. Next, calculate the two sided z-Values for:
   1. α = 0.05
   2. α = 0.35
   3. α = 0.65
   4. α = 0.95
3. Plot the z-Values that you calculated in the last part on the Standard Normal Curve. Use one color for each value of α.

Confidence Band

1. Assume we have a sample, with sample average x-bar, and standard error σ/√n. What are the Confidence Bands that correspond to the two sided z-Values that you just calculated.

Make sure you have labeled your charts neatly and appropriately. Also, make sure all of your charts are visible in your Workbook. Once you have completed all steps, save your Workbook as Project8.xls. You should email your instructor this .xls file.